Cette anisotropie est dénommée anisotropie magnétocristalline et provient de l'interaction électrostatique entre les orbitales des électrons responsables du magnétisme de l'atome et du champ électrique lié à la distribution de charges de l'environnement et dénommé champ cristallin. Cet effet d'anisotropie se manifeste au niveau du moment atomique global par l'intermédiaire du couplage spin-orbite qui rend donc indirectement le Spin sensible au champ cristallin.
Il s'ensuit donc que les substances dont les atomes magnétiques présentent un moment orbital L nul (on parle alors d'état S car ne subsiste que le moment de Spin) ou faible donneront lieu à une anisotropie magnétocristalline faible. Les composés issus du groupe du Fer, Nickel, Cobalt, réalisent ce cas de figure, soit parce qu'ils sont naturellement à l'état S (Mn2+, Fe3+), soit parce que leur moment orbital, conséquent à l'état libre, se trouve « éteint » par le champ cristallin.
A l'inverse, les composés issus des Terres rares présentent un moment orbital élevé et donneront lieu à des anisotropies magnétocristallines marquées liées à l'importance du couplage Spin-Orbite.
On rend compte de l'anisotropie magnétocristalline en exprimant la densité volumique d'énergie libre Fk qui lui correspond au moyen d'un polynôme développé en fonction des puissances croissantes paires des cosinus directeurs ai de l'aimantation, exprimés dans un repère lié à la maille cristalline. La valeur des coefficients associés aux différents monômes diminue très vite avec l'ordre de ceux-ci, de sorte qu'on se limite généralement au premier ou aux deux premiers termes du développement. L'expression analytique est fonction de la symétrie cristalline.
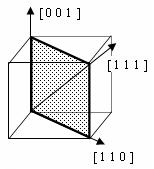
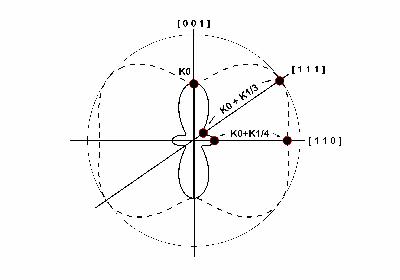
Figure 1 : Représentation polaire de la densité d'énergie d'anisotropie magnétocristalline pour une symétrie cubique réalisant K2 = 0, pour une direction d'aimantation contenue dans le plan contenant les trois directions principales. L'énergie étant définie à une constante près, on attribue à la direction [001] l'énergie K0 afin de faciliter la représentation.
Pointillés (K1>0) : les directions faciles sont les arêtes de la maille, les directions difficiles coïncident avec les grandes diagonales.
Trait continu (K1<0) : les directions faciles sont les grandes diagonales, les directions difficiles coïncident avec les arêtes.
Cas des systèmes cubiques
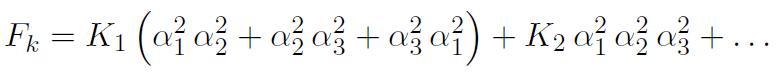
Si K1 est positif, alors les directions faciles sont les arêtes du cube -cas du fer-, alors que pour K1 négatif, les directions faciles sont les grandes diagonales du cube (cas du Nickel).
On peut illustrer sur le cas particulier de l'alliage FeSi utilisé dans les toles de transformateurs (3% Si en masse) la signification concrète de cette énergie : avec K1 = 3,5 104 J / m3, on devra fournir pour faire passer l'aimantation de la direction facile 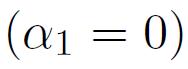
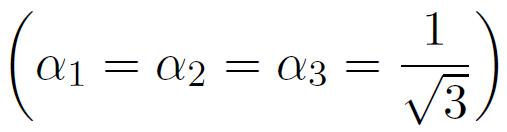
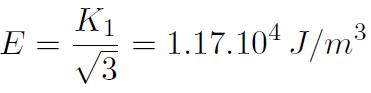
Cas des systèmes de basse symétrie
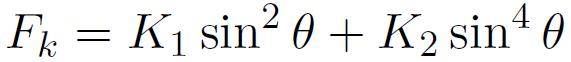
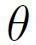 représente l'angle entre la direction d'aimantation et l'axe principal.
représente l'angle entre la direction d'aimantation et l'axe principal.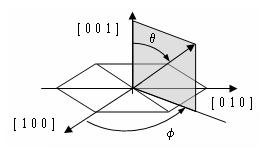
Figure 2 : repérage des directions dans une symétrie hexagonale. L'angle f n'intervient qu'au niveau du troisième terme du développement de Fk
Limitée à l'ordre 2, cette formulation coïncide avec l'expression de la densité d'énergie magnétocristalline pour les systèmes quadratiques ou rhomboédriques. Limitée au premier terme, cette expression donne une densité d'énergie d'anisotropie uniaxiale, généralement obtenus suite à un recuit effectué sous champ magnétique ou contraintes appliquées. On parle alors d'anisotropie induite, ces traitements s'appliquant à des matériaux présentant une densité d'énergie magnétocristalline intrinsèque très faible (Fk<100 J/m3) tels que alliages FeNi de type Permalloys, ou amorphes et nanocristallins doux.
De manière générale, on remarque que l'anisotropie magnétocristalline est plus marquée dans les systèmes de basse symétrie que dans les systèmes de haute symétrie. C'est ainsi que dans le cas du cobalt, avec K1=53.10^4 J/m3, on devra fournir pour faire passer l'aimantation de la direction facile à une direction difficile l'énergie volumique E=Ku=53.10^4 J/m3, soit 45 fois plus que pour le FeSi. Pour parvenir à ce résultat, il aura fallu appliquer un champ d'excitation dans la direction difficile d'amplitude Hk=2K1/Js=616 kA/m. Hk est dénommé champ d'anisotropie.
Il s'ensuit donc que l'amplitude des effets d'anisotropie est en premier lieu conditionnée par la catégorie à laquelle appartient l'élément concerné (éléments de transition 3d ou 4f) et ensuite déterminée par la symétrie présentée par le système étudié.
On peut enfin comparer l'amplitude du champ d'anisotropie au champ moléculaire. On peut illustrer le cas des composés 3d à l'aide du Cobalt, pour lequel on a µ0 Hk/Bmol= 4 pi 10-7 616/3,42 = 0,2 . Il apparaît clairement que les effets d'anisotropie sont sans commune mesure avec la force des interactions d'échange.
Ces effets sont pourtant de première importance vis-à-vis des applications : pour ce qui est de l'utilisation des matériaux doux, les champs d'excitation mis en œuvre sont de l'ordre de quelques 103 A/m (cas des machines tournantes), voire seulement quelques 102 A/m (cas des transformateurs de distribution) ou même beaucoup moins encore (disjoncteurs différentiels à hautes sensibilités) et donc tout à fait insuffisant pour imposer des directions d'aimantations hors des directions faciles, au moins pour les éléments purs. On contourne cette difficulté par la texturation des matériaux quand cela est possible (cas des tôles de transformateurs FeSi) ou en élaborant des alliages à faibles anisotropies, conditions pour lesquelles on obtiendra des alliages à hautes perméabilités. On s'intéressera alors plutôt aux matériaux réalisant des symétries cubiques, alors que réciproquement on choisira des matériaux à symétrie hexagonale pour réaliser des aimants.


