L'état quantique n, l, m, s
Les électrons sont distribués autour du noyau de l'atome et répartis dans différentes couches. Dans le modèle quantique, on ne caractérise pas les électrons par leurs trajectoires mais par leurs énergies. L'état d'un électron est défini par quatre paramètres n, , m, s, appelés les nombres quantiques atomiques :
-
Le nombre principal n prend des valeurs entières et correspond au numéro de la couche. Il détermine donc le numéro de la couche quantique à laquelle appartient l'électron.
-
Le nombre secondaire l peut prendre toutes les valeurs comprises entre 0 et n-1. Il détermine la sous-couche correspondante. Les sous-couches sont désignées par des lettres : s, p, d, f (pour croissant depuis 0).
-
Le nombre magnétique m peut prendre toutes les valeurs comprises entre - et . Il détermine le moment orbital de l'électron.
-
Le nombre de spin s ne peut prendre que les valeurs 1/2 et -1/2 et détermine la valeur du moment de Spin de l'électron.
Les régles de remplissage
Pauli a établi un principe d'exclusion qui porte son nom : deux électrons d'un même atome ne peuvent être dans le même état quantique et doivent donc différer par un des quatre nombres (n, , m, s). Une case quantique ne peut donc contenir que deux électrons au maximum, qui se différencient par la valeur de leur nombre s. On dit alors que les deux électrons sont appariés. Si une case quantique n'est occupée que par un électron, celui-ci est dit célibataire.
De manière générale, les électrons occupent les états de plus basse énergie disponibles et commencent par remplir les couches de numéros n les plus faibles et à l'intérieur d'une couche les sous-couches dans l'ordre croissant soit s, p, d... Malheureusement, les choses se gâtent à partir de la couche n° 3 dont des sous-couches présentent des niveaux d'énergie moindres que certaines sous-couches de la couche n°2 : on applique alors la règle de Klechkowski qui stipule que on remplit d'abord les sous-couches présentant le nombre n+ le plus faible avec, pour départager, n le plus petit possible (on note cependant quelques exceptions à cette règle comme Cr ou Cu ).
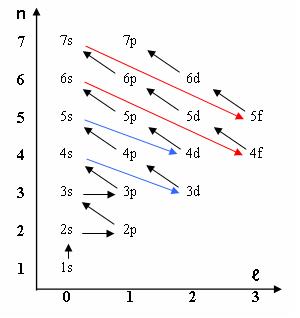
Figure 1 : Illustration de la règle de Klechkowski
Propriétés magnétiques de l'atome à l'état libre
Le moment magnétique de l'atome résulte des moments magnétiques individuels des électrons, eux-mêmes liés, on l'a vu, aux nombres quantiques mi et si (l'indice idénombre les électrons). Dans le cadre du couplage de Russel-Sanders, les moments individuels s'additionnent pour donner les moments résultants orbitaux et de Spin , proportionnels aux nombres quantiques L et S qu'on obtient simplement selon :
Enfin, du fait du couplage Spin-Orbite, les moments résultants et se combinent à leur tour pour donner le moment cinétique de l'atome proportionnel au nombre quantique J.
Le moment magnétique absolu de l'atome a pour amplitude :
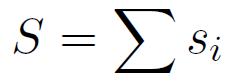
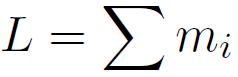
Le moment magnétique absolu de l'atome a pour amplitude :
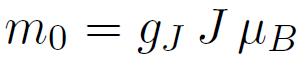
Où µB=9,273.10-24 Am2 désigne le magnéton de Bohr et gj le facteur de Landé :
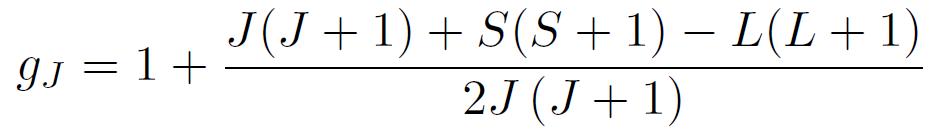
Les configurations électroniques les plus stables sont déterminées par les règles de Hund. Celles-ci stipulent que :
- La répartition maximise le moment de Spin, en accord avec le principe d'exclusion de Pauli.
- La répartition maximise le moments orbital, en accord avec le principe d'exclusion de Pauli et la première règle de Hund.
- Pour une couche plus qu'à moitié pleine, on a J=L+S, alors que pour une couche moins qu'à moitié pleine, on a J=|L-S|.
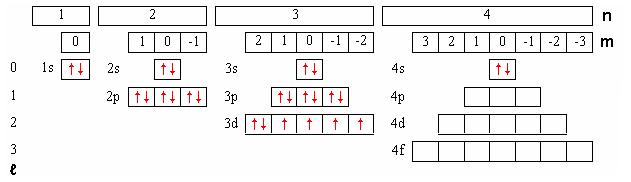
Figure 2 : Représentation des cases quantiques associées aux différentes sous-couches et exemple de remplissage pour l'atome de Fer (Z=26). L'orientation des flèches indique la valeur du nombre de spin (± ?). Conformément à la règle d'exclusion de Pauli, une case quantique ne peut être occupé que par deux électrons au maximum, qui doivent présenter des spins opposés. Le remplissage de la sous-couche incomplète 3d obéit aux règles de Hund. On obtient alors la structure électronique 1s2 2s2 2p6 3s2 3p6 4s2 3d6 et les nombres quantiques caractéristiques des propriétés magnétiques de l'atome à l'état libre S=2 L=2 J=4
Responsable
Olivier GEOFFROY