
Les matériaux nanocristallins doux sont les derniers-nés des matériaux dits ultra-doux, matériaux de très haute perméabilité. Plusieurs familles existent, et nous ne parlerons ici que de la famille « Finemet », et dont la société Arcelor-Mittal Imphy a mis au point des nuances propres produites sous l'appellation « Nanophy ».
De composition typique Fe75.3Cu1Nb2.84Si14.6B6.2, ces matériaux présentent une anisotropie magnétocristalline et une magnétostriction évanescente. Ils sont à ces titres comparables aux alliages de Fer-Nickel de type Permalloy et les amorphes à base Cobalt, mais présentent l'avantage par rapport à ces derniers d'avoir une aimantation à saturation plus élevée (1.3 T au lieu de 0.7T typiquement).
Elaboration
Elle s'effectue en deux étapes :
- Obtention d'un ruban amorphe par une technique de trempe sur roue
- Recuit de cristallisation autour de 500°C
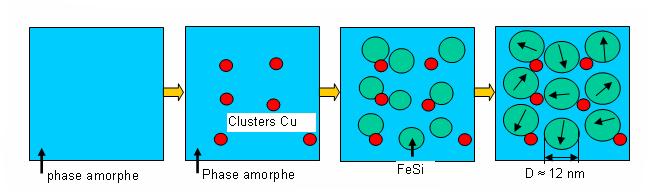
Figure 1 : Evolution de la structure cristalline au cours du recuit. Le cuivre favorise la multiplication des points de nucléation alors que la barrière de diffusion caractéristique du Niobium inhibe la croissance des grains au-delà du nanomètre
Propriétés d'anisotropie
A la fin du recuit les rubans sont composés d'un assemblage de nano-grains de Fer-Silicium d'orientation aléatoire, noyés dans une matrice résiduelle amorphe représentant environ 30% du volume total (cf. figure 1). Cette structure peu banale leur confère une anisotropie effective évanescente, propriété expliquée par le modèle de l'anisotropie aléatoire.
Sans entrer dans les détails du modèle, on retiendra que les différentes échelles auxquelles on est confronté concernent l'échelle du nanograin, caractérisé par une anisotropie magnétocristalline dont l'amplitude K0 est de l'ordre de 8000 J/m3 pour les nanograins FeSi, et l'échelle de la paroi de Bloch, qui nous amène à définir l'anisotropie effective Keff.
Pour un matériau cristallin classique, une paroi se déroule dans un milieu homogène de sorte que K0 et Keff sont identiques. Il en va autrement pour les matériaux nanocristallins, qui réalisent une épaisseur de paroi bien supérieure à la taille d'un nanograin (cf. figure 2). Ceux-ci présentant des directions cristallographiques aléatoires, on obtient par moyennage un milieu d'anisotropie effective évanescente.
Il s'agit là d'une caractéristique essentielle, car c'est précisément l'anisotropie effective qui va constituer l'ingrédient que l'on va retrouver dans les paramètres clefs que sont l'épaisseur de la paroi ep et son énergie surfacique w
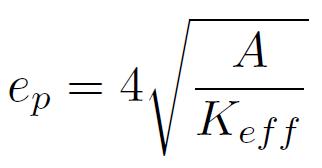
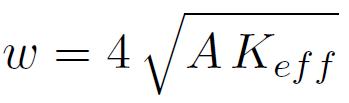
A désigne la constante d'échange ferromagnétique. Par voie de conséquence, Keff détermine également les propriétés macroscopiques de l'aimantation, comme par exemple la coercitivité Hc ou la perméabilité µr
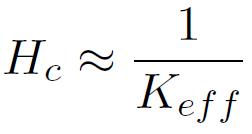
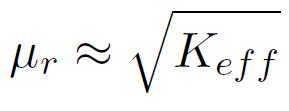
On obtient ainsi de très hautes perméabilités (µr>300 000) et de très faibles coercitivités (Hc<0.5 A/m), performances qui rangent les nanocristallins dans la catégorie très fermée des matériaux magnétiquement ultra-doux.

(a)

(b)
Figure 2 : situation d'une paroi dans les matériaux cristallins classiques (a) ou nanocristallins (b)
Un point important est que l'évanescence de l'anisotropie effective rend d'autres termes d'anisotropie (anisotropie d'origine magnéto-élastique ou anisotropie induite par le biais de champs magnétiques appliqués durant les traitements thermiques, voir illustration sur la figure 3) influents sur les propriétés d'aimantation, propriété qui peut être mise à profit pour la mise au point de capteurs et de bien d'autres fonctionnalités mais qui rend également les propriétés d'aimantation très sensibles aux conditions de mise en œuvre.
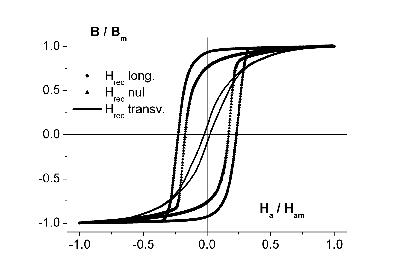
Figure 3 : Illustration sur un nanocristallin Finemet des effets d'anisotropie induits par un recuit sous champ magnétique sur la structure en domaines et conséquence sur le cycle d'hystérésis
Autres propriétés
Si l'évanescence de l'anisotropie effective constitue un préalable pour l'obtention des très hautes perméabilités, cette condition reste insuffisante. En effet, si la magnétostriction est élevée (par exemple de l'ordre de 10-5), on aura des propriétés d'aimantation conditionnées par les contraintes magnéto-élastiques qui peuvent être liées au conditionnement (appliquées par un éventuel enrobage protecteur par exemple) ou être générées par le matériau lui-même lors des processus d'aimantation. Les alliages nanocristallins, tout comme leurs concurrents, réalisent ainsi une magnétostriction très faible :
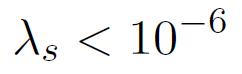
obtenue par simple compensation entre la magnétostriction de la phase amorphe :
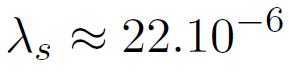
et de la phase cristalline :

Les nanocristallins Finemet réalisent par ailleurs une polarisation magnétique à saturation de l'ordre de Js=1.3 T, ce qui constitue un avantage décisif par rapport à leurs concurrents.
Enfin, ils réalisent une épaisseur e=18 m (une conséquence directe de leur mode d'élaboration) et une résistivité élevée (pour un alliage métallique) :
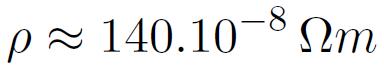
ce qui leur confère un excellent comportement dynamique et leur ouvre les portes des applications moyennes fréquences caractéristiques de l'électronique de puissance (quelques dizaines de kHz voire bien plus au moyen de traitements sophistiqués).
Bibliographie
- Y. Yoshizawa, S. Oguma and K. Yamauchi, J. Appl. Phys., 64: 6044 (1988)
- G. Herzer, IEEE Trans on Mag., 25: 3327 (1989)
- G. Herzer, IEEE Trans on Mag., 26: 1397 (1990)
- G. Herzer, J. Magn. Magn. Mater., 112: 258 (1992)
- O. Geoffroy, L. Fratila, J.-L. Porteseil, T. Waeckerlé, rev. Métal.-CIT/Sc. Gén. mat., (2003)
- O. Geoffroy, H. Chazal, J.L. Porteseil, T. Waeckerlé, F. Alvès, J. of Magn. Magn. Mater. 304(2): 145 (2006)

