MADEA : Parois de Bloch

Les parois de Bloch sont les zones de transition séparant les domaines magnétiques de Weiss.

Nous allons déterminer les caractéristiques d'une paroi de séparation dans le cas d'un échantillon dont les domaines sont orientés selon les directions Ux et -Ux (il s'agira donc ici d'une paroi à 180°, l'axe coïncidant avec une direction d'aimantation facile). Le cristal est ici supposé infini selon Ux et Uy.

L'amplitude du moment magnétique atomique étant, à température donnée, constante, la zone de transition se caractérise par une rotation progressive du moment entre atomes proches voisins depuis la direction initiale jusqu'à la direction opposée.  Afin d'éviter la création de masses magnétiques coûteuses en énergie magnétostatique, la polarisation doit réaliser la condition div(J) = 0. Le système étant invariant selon Ox et Oy, cela impose que la direction de l'aimantation est contenue dans les plans parallèles au plan Oxy.

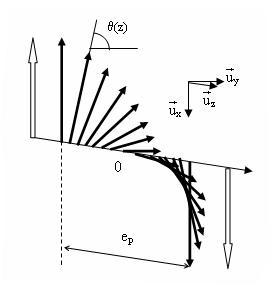
Le moment décrit donc une hélice d'axe Oz, la largeur ep de la paroi étant gouvernée par deux termes d'énergie antagonistes : sous l'influence des interactions d'échange ferromagnétiques, ep tend à croître infiniment, deux atomes proches voisins ayant tendance à rechercher le parallélisme des moments, alors que l'anisotropie magnétocristalline tend à promouvoir une paroi de faible épaisseur, les directions d'aimantations intermédiaires étant coûteuses en énergie. On formalise les choses en écrivant la densité d'énergie volumique d'échange à l'aide des cosinus directeurs ai de l'aimantation selon :

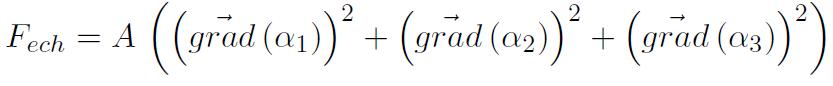
A désigne la constante d'échange ferromagnétique et est généralement de l'ordre de 10-11 J/m. Dans le cas présent, cette relation s'écrit simplement sous la forme :

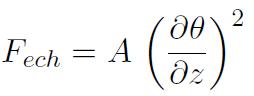
Un calcul variationnel permet par ailleurs d'établir que en tout point de la paroi la densité d'énergie d'échange est égale à la densité d'énergie d'anisotropie.

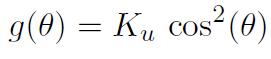
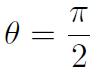
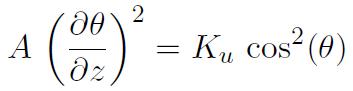
avec Ku>0 en considérant la direction  comme direction d'aimantation facile (cas de la figure 1). On obtient donc la relation :

En prenant l'origine des abscisses au centre, on en déduit l'équation du profil de la paroi :

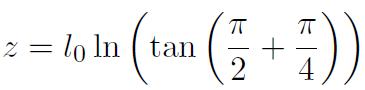
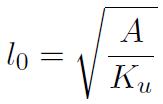
L'épaisseur ep de la paroi est de l'ordre de 4lo. Le paramètre lo est appelé longueur de corrélation ferromagnétique et revêt une importance considérable, puisqu'il quantifie l'ordre de grandeur de la distance minimale nécessaire dont il faut  s'écarter d'un point donné pour que l'on puisse observer une variation significative de la direction d'aimantation.

De manière logique, on vérifie que la paroi sera d'autant plus épaisse que le paramètre A - représentatif des interactions d'échange - est grand et que le paramètre Ku - relatif à l'anisotropie magnétocristalline - est petit.

Le profil de la paroi étant déterminé, on obtient facilement l'expression de l'énergie d'une paroi de surface unité selon :

 

 

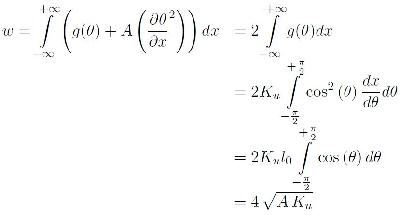
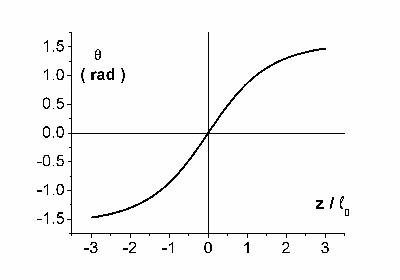
Figure 2 : Profil de paroi à 180 ° dans un  cristal uniaxial

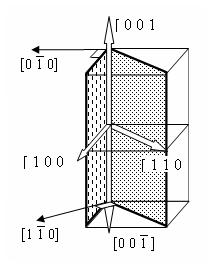
Figure 3 : Différentes orientations possibles pour une paroi à 180 ° dans un cristal cubique.

Comme le montre la figure 3, l'aimantation d'une paroi à 180° qui sépare deux domaines aimantés suivant [001] et [00-1] passe par une direction d'aimantation intermédiaire [100] facile si son plan est normal à la direction [0-10] alors que l'aimantation d'une paroi dont le plan est perpendiculaire à la direction [1-10] passe par une direction intermédiaire [110] plus difficile. L'épaisseur d'une paroi à 180° reste de l'ordre de 4 o, alors que l'énergie superficielle s'écrit :

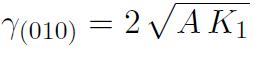
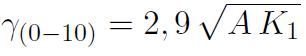
Dans le cas du fer, caractérisé par la constante d'échange A = 1,5 10-11 J/m et une constante principale d'anisotropie K1 = 4,8 104 J/m3, on obtient ainsi des parois à 180° d'énergie w ~ 2 10-3 J/m2 et d'épaisseur ep ~ 70 nm. Pour les matériaux les plus doux, caractérisés par des densités d'énergie d'anisotropie de l'ordre de 10 J/m3 (cas des alliages FeNi de type Permalloys par exemple), on obtient une épaisseur de paroi de l'ordre de quelques microns.