
Nous étudions le phénomène de multiplication de parois de Bloch sous l'action des courants induits développés en régime d'aimantation dynamique. On utilise pour cela des échantillons nanocristallins ultradoux de type Nanophy fournis par l'entreprise ArcelorMittal Imphy.
Principe physique de la multiplication des parois de Bloch
Les matériaux magnétiques sont constitués de domaines de polarisation magnétique uniforme appelés domaines de Weiss, séparés par des parois de Bloch (en rouge sur la figure 1(a)). Sous l'effet d'un champ appliqué, les parois se déplacent occasionnant dans les zones balayées des variations d'aimantation. Des forces électromotrices proportionnelles à la vitesse des parois en résultent et des boucles de courants induits (en vert sur la figure 1(b)) sont générées autour des parois en mouvement. Comme dans un solénoïde épais, ces boucles de courant génèrent un champ d'excitation induit Hj, et finalement une force de freinage F (en mauve sur la figure 1(a)).
Un point important est que la force de freinage F est plus forte dans la partie centrale que au voisinage de la surface du ruban. En fonction de sa rigidité, donc de son énergie w, la paroi se déforme alors (figure 1(b)) pour finir par se casser (figure 1(c)) quand Ha atteint une valeur critique Hcr proportionnel à l'énergie de la paroi.
Cet effet de cassure engendre une augmentation brutale du nombre de parois et des modifications importantes du cycle d'hystérésis.
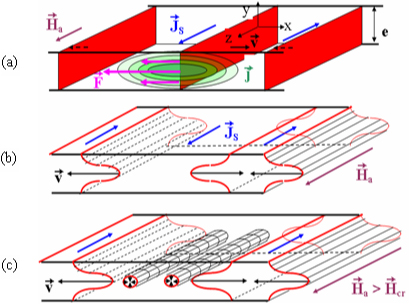
Figure 1 : Déplacement des parois de Bloch sous l'effet d'un champ appliqué d'amplitude croissante, (a) parois planes, (b) parois déformées et (c) brisure et multiplication des parois pour Ha > Hcr
Etude expérimentale
On relève les cycles d'hystérésis B(Ha) obtenus à l'aide d'un banc de caractérisation fluxmétrique (figure 2). Les échantillons sont désaimantés avant chaque expérimentation. On gomme ainsi l'histoire passée de manière à garantir la reproductibilité des phénomènes observés.
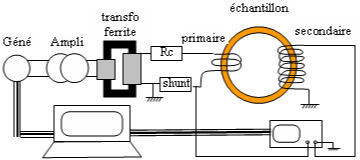
Figure 2 : Acquisition des signaux courant (tension aux bornes du shunt) et tension secondaire, permettant de remonter respectivement aux champs d'excitation Ha et à l'induction B
Protocole de base
A une fréquence donnée, on décrit des cycles d'hystérésis successifs pour des excursions de champ appliqué Ham croissantes, le but étant de déterminer l'excursion que l'on identifiera à Hcr pour laquelle un changement brutal se produit sur le cycle ou sur la perméabilité d'amplitude µ = Bm/Ham.
On travaille avec des excursions d'aimantations limitées à Js/2 afin que l'annihilation des parois qui accompagne l'entrée en saturation ne masque pas l'effet de la multiplication de parois. Il s'ensuit que la multiplication n'apparaît qu'au-delà d'une certaine fréquence d'aimantation.
La figure 3 montre la réalité du phénomène, obtenu ici pour une fréquence f = 30 kHz. La série de 14 cycles représentée est obtenue en augmentant progressivement Hmax. On a entre deux cycles successifs un incrément DBmax/Bmax de 0.2 % comparable à l'incrément DHmax/Hmax (cycles 1 à 7 et 8 à 14). Le passage du cycle 7 au cycle 8 se caractérise par un incrément DBmax/Bmax de 22 %. On évalue ainsi le champ critique Hcr = 8 A/m.
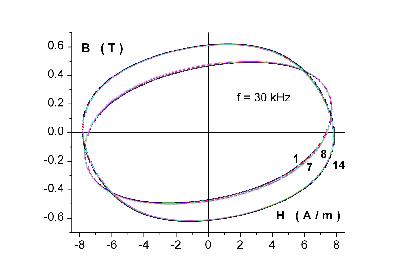
Figure 3 : Illustration du phénomène de multiplication.
Automatisation de la procédure
On peut caractériser la multiplication à l'aide d'un protocole plus aisé à mettre en œuvre : on génère pour cela une onde d'excitation constituée de 500 périodes, d'amplitude lentement croissante et on enregistre de manière synchronisée le signal secondaire.
L'analyse des enveloppes permet de repérer l'apparition de la multiplication, trahie par un accident sur la réponse enregistrée au bobinage secondaire de l'échantillon (figure 4).
La figure 4(a) représente l'évolution temporelle du champ H avec sa montée en rampe caractéristique alors que la figure 4(b) représente l'évolution temporelle de la tension secondaire, proportionnelle à dB/dt. On voit nettement la multiplication, celle-ci étant matérialisée par une brutale diminution de l'amplitude du signal tension.
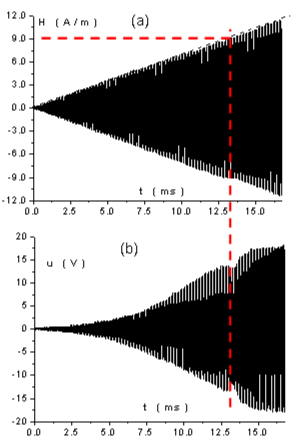
Figure 4 : Mesure automatisée (f=30 kHz) (a) évolution temporelle de H et (b) évolution temporelle du signal secondaire
Utilisation du phénomène de multiplication pour sonder les propriétés matériaux
Ces investigations présentent pour les matériaux nanocristallins un intérêt spécial :
Le Random Anisotropy Model montre en effet qu'il faut substituer au concept d'anisotropie magnétocristalline, l'anisotropie effective Keff. La valeur de Keff est le résultat d'un moyennage qui n'est perceptible qu'à l'échelle de la paroi de sorte que cette grandeur clef ne peut être appréhendée qu'au travers de manifestations mettant en jeu les parois. L'effet de multiplication est donc particulièrement bien indiqué pour déterminer cette grandeur. On formalise les choses de la manière suivante :
On montre en premier lieu que Hcr s'exprime en fonction de l'énergie w de la paroi, de la polarisation à saturation Js et de l'épaisseur e selon :
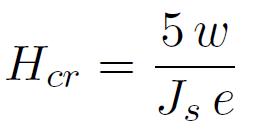
On connaît par ailleurs, pour un matériau cristallin classique, l'expression de l'énergie de paroi en fonction de la constante d'échange ferromagnétique A et de la constante d'anisotropie magnétocristalline K0 :
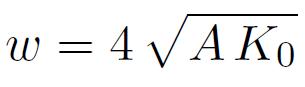
Pour les matériaux nanocristallins, on remplace dans l'expression précédente la constante cristalline K0 par l'anisotropie effective Keff. On obtient alors la relation
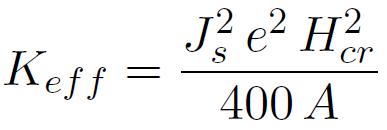
La figure ci-dessous établit ainsi de manière expérimentale une relation de proportionnalité entre le champ coercitif et l'anisotropie effective dépouillée d'après nos expérimentations basées sur la détermination des champs de multiplication.
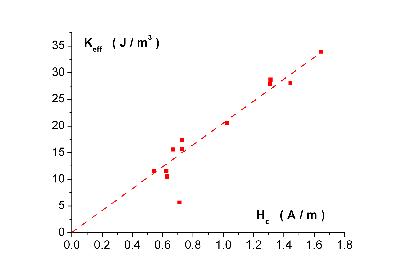
Figure 5 : Etude de la relation entre le champ coercitif Hc et la valeur de l'anisotropie effective Keff établie d'après la mesure de Hcr
Visualisation de plusieurs ordres
Nous présentons, figure ci-dessous, l'observation de deux champs Hcr successifs caractérisés selon le protocole automatisé. Cette observation a été effectuée à une fréquence de 30 kHz.

Figure 6 : Observation de 2 ordres successifs de multiplication ( f = 30 kHz)
On observe un premier champ de multiplication Hcr1=8 A/m et un second Hcr2=15 A/m. Hcr1 est mieux défini que Hcr2, sans doute parce que ce deuxième seuil s'établit au sein d'une population de parois déjà bien perturbée par la première multiplication.
Bibliographie
- W.J. Carr, J. Appl. Phys., 47(9): 4176 (1976)
- C. Beatrice et al, Journal de physique, Colloque C8, Sup. n°12, 49 (1988)
- C. Beatrice and al, IEEE Trans on Mag., 26(5): 1412 (1990)
- A. Maraner and al, J. Appl. Phys., 75(8): 4117 (1994)
- O. Geoffroy, L. Fratila, J.-L. Porteseil, T. Waeckerlé, rev. Métal.-CIT/Sc. Gén. mat., (2003)
- O. Geoffroy, H. Chazal, J.L. Porteseil, T. Waeckerlé, F. Alvès, J. of Magn. Magn. Mater. 304(2): 145 (2006)
- O. Geoffroy, H. Chazal, T. Waeckerlé, Matériaux 2006, Dijon (France), 13-17 Novembre 2006
- O. Geoffroy, M. Weiss, T. Waeckerlé, Matériaux du Génie Electrique, Toulouse (France), 15 et 16 Mai 2008

